Kita tahu teorema kecil fermat menyatakan
Nah..sekarang bagaimana jika modulusnya tidak prima, composite, apakah teorema kecil fermat masih berlaku?
Tidak, sebgai contohnya jika kita ambil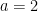 dan
dan  ,
,
apakah
Tidak karena 15 tidak membagi .
.
Akan tetapi ada cara memodifikasi teorema kecil fermat sehingga tetap berlaku meskupun modulusnya tidak prima. Teorema fermat yang udah dimodifikasi inilah yang disebut teorema euler.
Tidak, sebgai contohnya jika kita ambil
apakah
Tidak karena 15 tidak membagi
Akan tetapi ada cara memodifikasi teorema kecil fermat sehingga tetap berlaku meskupun modulusnya tidak prima. Teorema fermat yang udah dimodifikasi inilah yang disebut teorema euler.
Nah..sebelum membahas teorema euler akan saya bahas mengenai fungsi euler-phi
Definisi: Fungsi phi-euler, adalah fungsi pada bilangan asli  yang didefinisikan sebgai berikut
yang didefinisikan sebgai berikut
Contoh:  karena ada 4 bilangann asli yang kurang dari 8 yang coprime ke 8 ke-4 bilangan tersebut adalah 1,3,5,7.
karena ada 4 bilangann asli yang kurang dari 8 yang coprime ke 8 ke-4 bilangan tersebut adalah 1,3,5,7.  kerna semua bilangan pada
kerna semua bilangan pada  coprime ke 11.
coprime ke 11.
Teorema
- Jika
prima maka
- Jika
prima dan
maka
Bukti
1. Jika 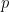 prima maka semu bilangan pada
prima maka semu bilangan pada  coprime ke
coprime ke 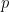 , itu artinya
, itu artinya 
2. Ada elemen pada himpunan
elemen pada himpunan 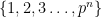 . Elemen pada himpunan tersebut tidak coprime ke
. Elemen pada himpunan tersebut tidak coprime ke 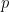 jika hanya jika dapat dibagi oleh
jika hanya jika dapat dibagi oleh 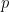 . Elemen pada himpunan yang dapat dibagi oleh
. Elemen pada himpunan yang dapat dibagi oleh 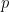 adalah
adalah
2. Ada
Ada sebanyak  elemen yang tidak coprime ke
elemen yang tidak coprime ke 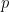 maka banyaknya elemen yang coprime ke
maka banyaknya elemen yang coprime ke 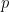 sebanyak
sebanyak 
Definisi: Sistem residu tereduksi mod  (reduced residue system mod
(reduced residue system mod  ) adalah himpunan bilangan-bilangan
) adalah himpunan bilangan-bilangan
Yang memenuhi
- Jika
maka
- Untuk setiap
coprime ke
Dengan demikian Sistem residu tereduksi mod  merepresentasikan bilangan-bilangan yang coprime ke
merepresentasikan bilangan-bilangan yang coprime ke 
Contoh:  dan
dan  keduanya merupakan sistem residu tereduksi mod
keduanya merupakan sistem residu tereduksi mod 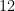
Lemma: Diberikan  dan
dan  adalah Sistem residu tereduksi mod
adalah Sistem residu tereduksi mod  , berlaku:
, berlaku:
- Untuk semua bilangan bulat
maka
merupakan sistem residu tereduksi mod
.
- Jika
coprime ke
maka
merupakan sistem residu tereduksi mod
.
Akibat: Diberikan  dan
dan  adalah Sistem residu tereduksi mod
adalah Sistem residu tereduksi mod  , jika
, jika  coprime ke
coprime ke  dan
dan 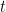 sebarang bilangan bulat maka
sebarang bilangan bulat maka  merupakan sistem residu tereduksi mod
merupakan sistem residu tereduksi mod  .
.
Contoh: 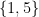 merupakan sistem residu tereduksi mod
merupakan sistem residu tereduksi mod 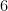 . tmabahkan
. tmabahkan  pada setiap bilangan diperoleh
pada setiap bilangan diperoleh  , sistem residu tereduksi mod
, sistem residu tereduksi mod 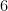 lainnya, Kita tahu 6 coprime ke 25, jika kita kalikan sistem yang awal dengan 25 diperoleh
lainnya, Kita tahu 6 coprime ke 25, jika kita kalikan sistem yang awal dengan 25 diperoleh 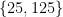 istem residu tereduksi mod
istem residu tereduksi mod 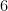 lainnya, terakhir
lainnya, terakhir  juga merupakan sistem residu tereduksi mod
juga merupakan sistem residu tereduksi mod 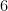
Selanjutnya kita bahas teorema euler
Teorema Euler: Setiap bilangan bulat  dan
dan  bilangan bulat positif yang coprime ke
bilangan bulat positif yang coprime ke  maka
maka
Perhatikan jika  prima maka
prima maka  ,
teorema euler berubah menjadi teorema kecil fermat. Dengan demikian
kita bisa menganggap teorema euler sebagai generalisasi teorema kecil
fermat.
,
teorema euler berubah menjadi teorema kecil fermat. Dengan demikian
kita bisa menganggap teorema euler sebagai generalisasi teorema kecil
fermat.
Bukti: Ambil  dan
dan  adalah Sistem residu tereduksi mod
adalah Sistem residu tereduksi mod  , diasumsikan
, diasumsikan  termuat di
termuat di  .
.
Karena  dan
dan  coprime maka
coprime maka  juga merupakans sistem residu tereduksi mod
juga merupakans sistem residu tereduksi mod  , Kedua sistem tersebut haruslah mempunyai hasil perkalian modulus
, Kedua sistem tersebut haruslah mempunyai hasil perkalian modulus  yang sama
yang sama
Karean setiap  coprime ke
coprime ke  , jika dikalikan kedua sisi dengan
, jika dikalikan kedua sisi dengan  diperoleh
diperoleh